免责声明:
本站部份内容系网友自发上传与转载,不代表本网赞同其观点;
如涉及内容、版权等问题,请在30日内联系,我们将在第一时间删除内容!

标准号:GB/T 510-2018 中文标准名称:石油产品凝点测定法前言本标准按照GB/T1.1一2009给出的…
150 万私域用户案例详解: 怎么快速构建流量池,实现变现?一、案例前言今年,营销领域最热门…
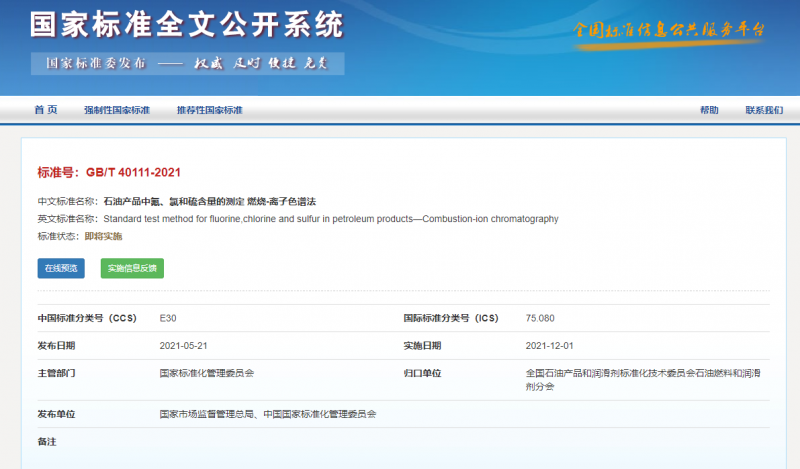
石油产品中氟、氯和硫含量的测定燃烧-离子色谱法警示一使用本文件的人员应有正规实验室工作的…

页岩气地质评价方法1 范围本标准规定了页岩气的定义、地质评价内容.方法和参数.本标准适用于…

产品名称: 硅脂膏,电缆附件硅脂,绝缘润滑脂 产品型号: GR300 产品商标: ECCO/埃科产品规…

产品名称:高导热硅脂,导热绝缘硅脂,高温导热硅脂 产品型号:GR320-BS 产品商标: ECCO/埃…
GLM-2406ZD智能化全自动触摸屏控制氧指数测定仪一)产品功能…
标准号:GB/T 510-2018 中文标准名称:石油产品凝点测定法前…
150 万私域用户案例详解: 怎么快速构建流量池,实现变现?一…
石油产品中氟、氯和硫含量的测定燃烧-离子色谱法警示一使用本…
页岩气地质评价方法1 范围本标准规定了页岩气的定义、地质评…
知级是一个操作简单、报告结果易懂的邮件地址验证工具,根据…
产品名称: 硅脂膏,电缆附件硅脂,绝缘润滑脂 产品型号: GR…
产品名称:高导热硅脂,导热绝缘硅脂,高温导热硅脂 产品型号…
耐高低温度特性:需要-40~+100不凝结不流失。普通黄油的低温…
7月初,在这举国欢庆百年大业的日子里,干我们这一行的也大都…